Chat!
How To Play Chess — player ratings
- Overview
- How to set up the board
- Moves
- How the pawn moves
- How the knight (also called the horse) moves
- How the bishop moves
- How the rook (also called the castle) moves
- How the queen moves
- How the king moves
- The object of the game
- Stalemate
- Draw
- Special Moves
- Pawn Promotion
- Piece Value
- Player Ratings
Player Ratings
You'll notice that throughout nothingbutchess.com, players are assigned a numerical rating. This is a value that indicates just how good a player is. Every player that signs up with nothingbutchess.com is given an initial rating of 1200. Their rating goes up or down based on wins, losses and ties and the rating of the person they played.
The steps used to calculate a person's rating are:
1. Compute the rating differences
2. Look up your win expectancy
3. Compare your expected score to your actual score
4. Determine your k-factor
5. Compute your new rating
Let's go through the steps above with two fictitious players. One has a rating of 1650 (player A) and the other has a rating of 1350 (player B). Let's say that the 1350 player pulled off the upset and won the game.
Compute the rating differences
Calculating the rating difference is simple. It's always your rating minus your opponent's rating. So they'd be
player A: 1650 - 1350 = 300
player B: 1350 - 1650 = -300
Look up your win expectancy
There is a formula which determines a user's win expectancy. It's a little complicated, but the tabulated results are below.
|
|
|
So looking at the table above, If one player's rating is 677 points (or more) greater than the other's they're win expectancy is .99. Translation: that player is expected to win 99% of the time. Conversely, if your opponent's rating is 677 points better than yours, you're only expected to win 1% of the time. If the rating difference is 0, you're expected to win 50% of the time and your opponent is expected to win 50% of the time, as one would expect.
Using the table above:
player A: rating difference 300 — Win Expectancy - 0.85
player B: rating difference -300 — Win Expectancy - 0.15
Compare your expected score to your actual score
A player gets either a 1 if they won, a 0 if they lost and 0.5 for a tie. Subtracting the expected win expectancy from the actual win expectancy gives each player an overall win expectancy.
player A: 0 - 0.85 = -0.85
player B: 1 - 0.15 = 0.85
Determine your k-factor
Rather than discuss how this value is determined, let's just talk about how things are done at nothingbutchess.com. If your rating is less than 2200, it's 24. If it's over 2200, it's 16. When you see the final formula, what this will mean is that it becomes harder to increase your rating once you get over 2200. Now if your rating gets that high, God bless you!
Compute your new rating
The formula (once all of the preparation above has been complete) is simply:
new rating = old rating + (k-factor * overall win expectancy)
The new ratings) (after rounding off) are:
player A: 1650 + (24 * -0.85) = 1630
player B: 1350 + (24 * 0.85) = 1370
Solve This Puzzle?
| 8 |  |  |  |  |  |  |  |  |
| 7 |  |  |  |  |  |  |  |  |
| 6 |  |  | 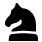 |  |  |  |  |  |
| 5 |  |  |  |  |  |  |  |  |
| 4 |  |  |  | 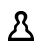 |  |  |  |  |
| 3 |  |  |  |  |  |  |  |  |
| 2 | 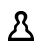 |  |  |  |  | 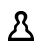 |  |  |
| 1 |  |  |  |  |  |  |  |  |
| A | B | C | D | E | F | G | H |
